Les trois lois de Newton

La mécanique de Newton repose sur les trois célèbres lois du mouvement définies au début du premier volume de Philosophiae Naturalis Principia Mathematica. Ces lois encore étudiées aujourd'hui dans les lycées sont présentées ci-dessous.

Première loi : principe d’inertie
Galilée énonce une forme imprécise du principe d’inertie suite à ses expériences sur un plan incliné :
« Un degré de vitesse quelconque, une fois communiqué à un mobile, s’imprime en lui de façon indélébile du seul fait de sa nature, et pourvu que soit supprimées les causes extérieures d’accélération et de ralentissement. »
Newton reformule le principe d’inertie de manière plus rigoureuse, en ajoutant les termes exacts dans son ouvrage Principes mathématiques de la philosophie naturelle.
« Tout corps persévère dans l’état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n’agisse sur lui, et ne le contraigne à changer d’état. »
Cette loi montre qu’Aristote s’était trompé. Une force est obligatoire pour maintenir la vitesse d’un mobile. Newton illustre cette loi par le mouvement des projectiles, le mouvement des toupies, et le mouvement de rotation des planètes sur leur axe. Si le mouvement des projectiles est en accord avec le principe d’inertie, les deux autres exemples montrent que des corps mis en rotation, en l’absence d’autres forces, conservent leur vitesse de rotation. C’est la loi de conservation du moment cinétique que Newton ne distinguait pas du principe d’inertie.

Deuxième loi de Newton (loi fondamentale de la dynamique):
« Les changements qui arrivent dans le mouvement sont proportionnels à la force motrice, et se font dans la ligne droite dans laquelle cette force a été imprimée. »
Newton n’est pas très précis dans la formulation de sa loi. Il n’y a pas de référence au temps. On peut se demander si F=ma, c'est-à-dire si la force est proportionnelle à l’accélération ou si F=mΔv , la force est proportionnelle à la variation de vitesse.

Troisième loi (action/réaction):
« L’action est toujours égale et opposée à la réaction ; c'est-à-dire que les actions de deux corps l’un sur l’autre sont toujours égales, et dans des directions contraires. »
Alors que Hooke dit que le Soleil exerce une force sur les planètes, Newton affirme que les planètes exercent une force de même intensité et de sens contraire sur le Soleil.

La loi de gravitation universelle

Rapide survol des lois de Kepler sur les mouvements des planètes autour du Soleil :

Mais les théories de Kepler sont rejetées par ses contemporains en partie car les cinq planètes connues à l’époque ont une orbite quasi circulaire.

Newton se sert des recherches de ses prédécesseurs (Kepler, Descartes, Galilée…).
Les lois de Kepler rendent les trois lois de Newton universelles.
D’après les travaux de Descartes, Newton se demande quelle force retient les planètes sur leurs orbites.
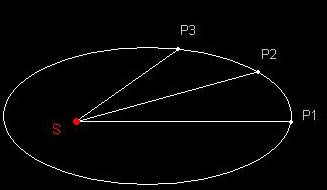
Dans les Propositions 1 et 2 du premier tome des Principia, Newton affirme que si un corps est soumis à une force centrale, sa trajectoire obéit à la loi des aires et réciproquement. Newton cherche à comprendre quelle est la nature de la force qui met en mouvement une planète. L’hypothèse est la suivante : un point P décrit une orbite elliptique dont S est un foyer et le vecteur SP balaie des aires égales durant des intervalles de temps égaux. (ZR) est une droite tangente en P à la trajectoire. Q est un point de la trajectoire, (SP) est parallèle à (QR) et perpendiculaire à (QT).

Newton commence par en déduire, d’après la Proposition 2, que la force qui agit sur P est centrale et dirigée vers S.
D’après les propriétés géométriques de l’ellipse, lorsque Q tend vers P, QR/QT²=constante (indépendante de P). Newton démontre cela dans « Prob.3 », De Motu.
Ensuite, Newton évalue géométriquement l’intensité de la force centrale. Le mouvement du corps lorsqu’il passe de P à Q n’étant pas rectiligne uniforme pendant l’intervalle de temps Δt, la force a varié d’intensité et de direction en arrivant en Q. Par approximation, on peut considérer que le corps est soumis à une force constante le long de l’arc PQ, si la distance PQ et Δt sont très petits.
On cherche alors la déviation QR pendant Δt. Galilée a mis en évidence qu’un corps soumis à une force constante dévie de sa trajectoire initiale, de telle sorte que sa distance de chute est proportionnelle au carré du temps de la chute multiplié par l’accélération.
N’ayant pas étudié l’accélération, nous allons simplement dire que d’après la deuxième loi du mouvement, l’accélération est proportionnelle à la force et donc d’après ce que nous avons vu ci-dessus: l’intensité F de la force est proportionnelle à la limite du rapport QR/(Δt)² quand Q tend vers P.
En termes géométriques, Δt est proportionnel à l’aire SPQ puisque la loi des aires est vérifiée. L’arc PQ est pratiquement confondu avec la corde reliant P à Q car il est très petit. Donc l’aire SPQ est égale à l’aire (SP×QT)/2 du triangle SPQ, et Δt est proportionnel à SP×QT. Par conséquent, F est proportionnelle à la limite du rapport QR/(SP×QT)² quand Q tend vers P.
F=QR/(SP×QT)² > F×1/SP² = QR/QT² or QR/QT² est une constante donc F est proportionnelle à 1/SP² ce que l’on peut traduire par l’intensité de la force est inversement proportionnelle au carré de la distance SP.
D’après les deux premières lois de Kepler et la force inversement proportionnelle au carré de la distance responsable du mouvement, Newton conclut que l’intensité de la force d’attraction entre deux corps de masses respectives m et M est proportionnelle au produit des masses et inversement proportionnelle au carré de la distance r qui les sépare, soit : F=G.(Mm/r²) où G est la constante universelle de gravité.

Mais la réponse à la question que Newton s’est initialement posée n’est pas résolue. A cette époque, certains physiciens et philosophes de la nature donnaient au mouvement des planètes une cause magnétique, ou celle de tourbillons de matière cosmique comme Descartes. Newton pense lui que cette force est la gravité. Il donne donc une cause commune aux mouvements des planètes et aux chutes d’objets sur Terre : c’est la théorie de la gravitation universelle. Pour démontrer cela calculons la « chute » de la Lune sur Terre et la chute d’une pomme au voisinage de la Terre pendant une seconde.

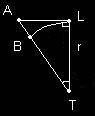
La Lune : Soit L l’emplacement initial de la Lune, T la Terre, r le rayon Terre-Lune, v la vitesse de la Lune sur sa trajectoire.
r=3.8.10^8m et v=1.10^3m/s.
S’il n’y avait pas d’attraction terrestre, la Lune continuerait sa trajectoire en ligne droite, (LA).
Mais en raison de l’attraction, elle chute d’une distance AB que l'on va apeller h. Sa véritable trajectoire est donc LB.

D’après le théorème de Pythagore :

AL²+LT²= AT² AL²+r²=(h+r)² AL²+r²=h²+2hr+r² les r² s’annulent. v=d/t ? v²=(AL/t)² où t=1 seconde donc v²=AL². v²=h²+2hr On calcule delta : Δ=b²-4ac Δ=2²-0=4 x1= (-b- racineΔ)2a = -2 . x2=(-b+ racineΔ)/2a = 0

h=v²/2r
hlune=(1.10^3)²/(2.3.8.10^8)=1.3.10^-3m/s=1.3mm.
La Lune chute de 1.3mm en 1 seconde.

Un objet au voisinage de la Terre chute d’environ 5m en 1 seconde ( en chute libre).
hpomme=5m
Le rapport des distances d’attraction de la Terre sur la Lune et de la Terre sur la pomme est :
r/Rterre=3.8.10^8/6.38.10^6=60
La Lune est 60 fois plus loin du centre de la Terre que la pomme.
Le rapport des hauteurs de chute de la pomme et de la Lune sont :
hpomme/hlune=5/1.3.10^-3=3600=60×60
La Lune est attirée 60×60 fois moins que la pomme.
Le mouvement de la Lune et la chute d’une pomme sur Terre sont régis par la même loi de l’attraction. La théorie de Newton est bien universelle.

Ces résultats sont illustrés par la fameuse expérience du tube de Newton. Ce tube est un simple tube dans lequel on fait le vide grâce à une pompe à vide. On place à l'intérieur du tube une plume et du plomb, un dispositif permet de lâcher simultanément les objets. N'ayant pas de frottements dûs à l'air dans le tube, la plume et le plomb atteignent le fond du tube en même temps. Cette expérience a aussi été réalisée sur la Lune lors de la mission Appolo 15 avec une plume et un marteau en 1971.

Cependant la dernière question que Newton se posait reste encore aujourd'hui inexplicable: quelle est la cause de la gravitation?